요즈음에는 미적분학 내용들을 복습하고 있습니다. 제가 처음 미적분학을 공부할 때 사용했던 교재는 미적분학 교재로는 stewart calculus 8th edition: metric edition 인데요, 1.1절에서는 미적분학의 본격적인 내용을 다루기에 앞서 함수의 정의에 대해 다루고 있습니다.
1.함수의 정의
함수의 정의는 우리 고등 수학 교육과정에도 있는 내용입니다. 함수의 정의는 아래와 같습니다.
공집합이 아닌 두 집합 X, Y에 대하여 집합 X의 각 원소에 집합 Y의 원소가 오직 하나씩만 대응할 때,이 대응을 X에서 Y로의 함수라 하고, 기호로 f: X->Y 와 같이 나타낸다.
'f: X->Y' 이 표시는 함수 f의 정의역은 X이고, 공역은 Y라는 것을 나타냅니다. 집합 X의 원소들을 집합Y 의 원소들에 대응되게 하는 어떤 관계 f라는 뜻이죠.
Stewart Calculus에는 함수가 다음과 같이 정의되어 있습니다.
집합 D에 있는 각각의 원소 x가 f(x)라고 불리는 집합 E에 있는,정확히 하나의 원소에 대응되도록 하는 규칙 f를 함수라고 한다.
A function f is a rule that assigns to each element x in a set D exactly one element, called f(x), in a set E.
James Stewart Calculus,metric edition,8th edtion>
함수에 대해 더 자세히 설명하기 전에, 다음과 같은 용어들을 설명하고 넘어가겠습니다.
정의역(Domain)=set D: 위의 함수의 정의에서 집합 D를 일컫는 말입니다. 함수에 입력되는 값들의 집합입니다. 정의역의 임의의 원소를 나타내는 문자로 x를 주로 사용합니다.
공역(Codomain)=set E: 위의 함수의 정의에서 집합 E를 일컫는 말입니다. 함수를 통해 정의역의 원소에 대응될 수 있는, 즉 함수의 결과값으로 가능한 값들의 집합입니다.
치역(Image): 집합 D의 원소들을 함수에 넣었을 때, 집합 E 안의 모든 원소들이 집합 D의 모든 원소에 대응하는 것은 아닙니다. 집합 E-공역-에 있는 원소들 중, 집합 D-정의역-에 있는 원소와 함수를 통해 대응하는 값들의 집합=함숫값 전체의 집합을 치역이라고 합니다. 식으로는 아래와 같이 나타낼 수 있습니다.
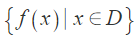
독립변수(Independent Variable) : 정의역에 있는 임의의 원소를 나타내는 기호 혹은 변수를 독립변수라고 합니다.
종속변수(Dependent Variable) : 치역에 있는 임의의 원소를 나타내는 기호 혹은 변수를 종속변수라고 합니다.
흔히 함수를 설명할때는 입력이 있으면 출력이 있는 기계 그림- input-output machine diagram을 자주 사용하고는 합니다. 함수란 하나의 입력이 있으면 하나의 출력만 나오는 기계라고 비유할 수 있다는 것입니다.
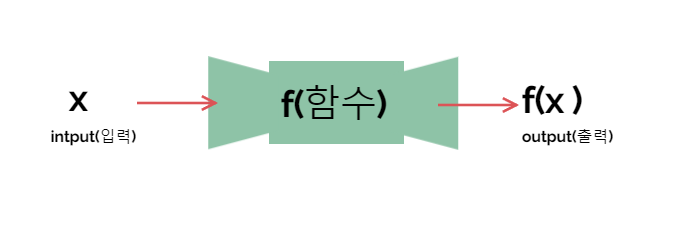
위 그림은 함수의 역할이 무엇인지 설명하는 대표적인 그림이라고 볼 수 있습니다. 아래 그림 역시 함수를 설명하는 그림입니다. 그러나 아래 그림이 함수가 어떻게 구성되는지 설명하는데 더 효과적인 그림이라고 저는 생각합니다.
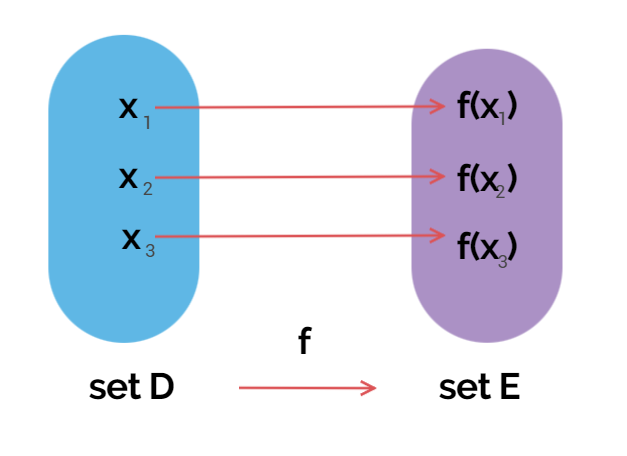
<arrow diagram>
이 그림은 arrow diagram 이라고 부릅니다. 아무래도 화살표로 정의역의 원소와 공역의 원소를 이은 그림이라 이런 이름이 붙었을 것입니다. 그림을 조금 더 자세히 살펴보겠습니다. 먼저 왼쪽의 파란색 영역은 set D, 즉 정의역이고, 오른쪽의 보라색 영역은 set E, 공역입니다. 정의역의 각각의 원소 x1 x2 x 3 는 공역의 원소 f(x1), f(x2), f(x3) 에 대응되고 있습니다. 이 경우 치역은 집합 { f(x1), f(x2), f(x3)} 입니다.
여기서 주의해서 기억해야 할 내용은, 함수에서 정의역의 한 원소에는 단 한개의 공역의 원소만 대응될 수 있다는 것입니다. 아래 그림을 살펴보겠습니다.
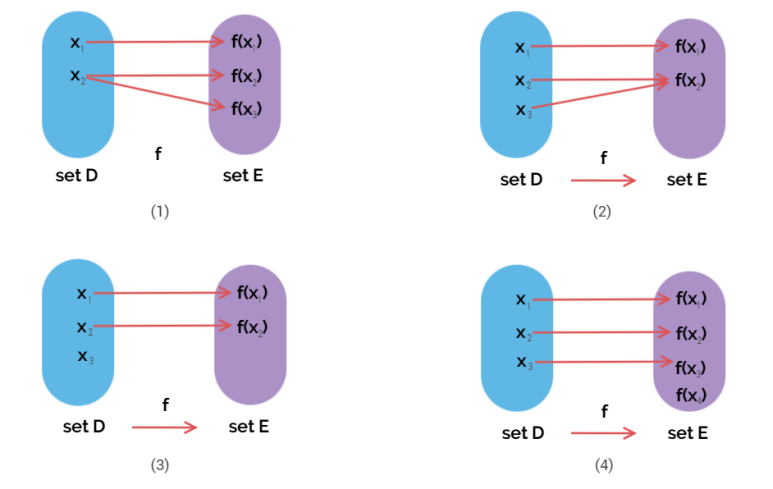
위의 네 그림 중 어떤 그림의 f가 함수이고 어떤 그림의 f가 함수가 아닌지 아시겠나요?
정답을 공개하겠습니다! 위 그림에서 (1),(3)은 함수를 나타내는 그림이 아니고, (2),(4) 는 함수를 나타내는 그림입니다.
먼저 (1)을 보겠습니다. 정의역의 원소 x2 에 대응한 공역의 원소가 f(x2), f(x3)로 총 두개입니다. 이는 정의역의 한 원소에는 공역의 원소 하나만 대응되어야 한다는 함수의 정의에 어긋나므로, (1)은 함수가 아닙니다.
두번째로 (2)를 살펴보겠습니다. 정의역의 원소 x2 x 3 는 둘다 공역의 원소 f(x2)에 대응되는데 함수가 맞냐고 생각하실 수 있습니다. 그러나, 정의역의 원소 x2 가 대응되는 공역의 원소는 f(x2)로 하나이고, x 3 가 대응되는 공역의 원소도 f(x2) 하나뿐이므로, 함수의 정의에는 어긋나지 않습니다.
다음은 (3)입니다. 다른 원소들은 공역의 원소 한개씩에만 대응하고 있습니다. 그러나 x 3 가 대응되는 공역의 원소가 없습니다. 함수에서는 정의역의 모든 원소가 대응되는 값을 가져야 합니다. 따라서 이 경우는 함수라고 부를 수 없습니다.
마지막으로 (4)를 보겠습니다. (4) 같은 경우는 당연히 함수라는 것을 알 수 있습니다. 공역의 모든 원소는 정의역에 대응될 필요가 없겠지요. 이 경우 공역은 {f(x1), f(x2), f(x3),f(x4) } 이지만, 치역은 공역과 달리 {f(x1), f(x2), f(x3)} 입니다. 그렇지만 정의역의 모든 원소가 각각 대응되는 값을 가지기 때문에 이 경우는 함수라고 볼 수 있습니다.
맨 처음 보여드린 arrow diagram은 일대일대응을 만족하는 함수입니다. 그림 (4) 같은 경우는 일대일함수이지만, 일대일대응은 아닙니다. 일대일대응과 일대일함수에 대한 내용은 나중에 추가로 다뤄보겠습니다.
2.동일한 함수의 조건
그렇다면 어떤 함수가 같은 함수이고, 어떤 함수가 다른 함수일까요? 두 함수가 서로 같을 조건은 아래와 같습니다.
1)정의역과 공역이 서로 같고
2)정의역의 모든 원소 x에 대하여 f(x)=g(x)
일때, 두 함수 f와 g는 서로 같은 함수입니다.
'수학 > 고등수학' 카테고리의 다른 글
| 함수의 극한-직관적 정의 (0) | 2023.08.14 |
|---|---|
| 일대일함수, 일대일대응 그리고 함수의 개수 (+상수함수, 항등함수) (0) | 2023.05.20 |

