일대일함수, 일대일대응 그리고 함수의 개수 (+상수함수, 항등함수)

 저번 글에서는 함수의 정의에 대해 다뤄보았습니다. 오늘은 함수의 정의에서 조금 더 나아가 특별한 조건을 만족하는 함수들인 일대일함수, 일대일대응 함수에 대해 알아보도록 하겠습니다. 그리고 추가로 상수함수와 항등함수에 대해서도 같이 설명하겠습니다.

 

그 전에, 함수의 정의에 대해 명확한 개념이 잡히지 않은 분들은 제가 저번에 쓴 함수의 정의 관련 아래 글을 참고하고 오늘 글을 읽어주시기 바랍니다.

 

함수의 정의

 

 

<왼쪽은 일대일 함수, 오른쪽은 일대일대응>

---

1. 일대일함수(one-to-one function)

 

 일대일함수란 말 그대로 정의역의 원소 하나에 공역의 원소 하나가 대응된다는 의미입니다. 서로 다른 정의역의 원소는 한 공역의 원소에 대응될 수 없기에 일대일함수라는 이름이 붙은 것입니다. 조금 더 엄밀한 정의를 살펴보겠습니다. 제목에도 나와 있듯, 일대일함수는 영어로 one-to-one function 이라고 부릅니다.

 

일대일함수(one-to-one function)의 정의:

함수 f: X->Y에서 정의역 D의 임의의 두 원소 x1, x2 에 대하여 x1≠x2일때 f(x1)≠f(x2) 이면, 함수f는 일대일함수라고 한다.

 

 일대일함수는 당연히 'x1=x2 이면 f(x1)=f(x2)' 조건도 만족합니다. 그렇다면 왜 정의를 이렇게 두지 않았을까요? 그 이유가 있습니다. 

 'x1=x2 이면 f(x1)=f(x2)' 가 함수 f가 일대일함수가 될 조건이라고 생각해 봅시다. 그렇다면 x1≠x2 인 경우에 f(x1)=f(x2) 라면 이 조건에 위배되는 경우일까요? 그렇지 않습니다. 그러나 이 경우에는 일대일함수라고 볼 수 없습니다. 왜냐하면 정의역의 원소 두개에 공역의 원소 하나가 대응되고 있기 때문입니다. 그러니 아래 그림과 같은 상황인 것입니다.

<이 경우는 일대일함수가 아니다>

 

 따라서, 일대일 함수의 정의를 위와 같이 둔 것입니다. 위의 정의에 나와있는 조건 x1≠x2일때 f(x1)≠f(x2) 의 대우는 'f(x1)=f(x2) 이면 x1=x2' 

라는 명제가 될 테니, 이 역시 일대일함수의 정의로 볼 수 있을 것입니다.

 

---

2. 일대일대응(one-to-one correspondence)

 일대일대응은 일대일함수의 진화형(?)이라고 할 수 있겠습니다. 무슨말이냐 하면, 아래 정의를 살펴보면 쉽게 이해가 되실 것입니다.

 

함수 f: X->Y가 일대일함수이고, 공역고 치역이 같을 때, 함수 f를 일대일대응이라 한다.

 일대일대응은 일대일함수의 조건을 만족하면서 , 그 중 공역과 치역이 같은 함수입니다. 아래 그림을 보겠습니다.

<일대일대응은 공역과 치역이 같다>

 

 일대일함수는 서로 다른 정의역의 원소에 대해 공역의 서로 다른 원소가 대응되는 함수입니다. 그러나 공역의 모든 원소가 정의역에 대응되어야 할 필요는 없습니다. 즉 공역과 치역이 서로 달라도 일대일함수일 수 있습니다. 

 

 일대일대응은 이런 일대일함수에 간단한 한가지 조건이 추가된 것입니다. 바로 공역=치역 이라는 조건입니다.

 

 따라서 일대일함수는 일대일대응이 되기 위한 필요조건입니다. 일대일대응이면 무조건 일대일함수이기 때문에 일대일대응은 일대일함수의 충분조건이고요. 일대일대응이면 무조건 일대일함수이지만, 일대일함수라고 해서 무조건 일대일대응은 아니라는 것입니다.

 

2.1 역함수를 가질 조건

 

 오로지 일대일대응 함수만 역함수를 가질 수 있습니다. 역함수라는 것은 기존의 함수의 공역을 새롭게 정의역으로 두고, 기존 함수의 정의역을 새롭게 공역으로 갖는 함수입니다. 

 

 그렇다면 왜 일대일대응 함수만 역함수를 가질 수 있을까요? 이유는 아래 그림을 보면 쉽게 이해할 수 있습니다.

 

<맨 위는 일대일대응 함수로 역함수를 성공적으로 만들어낸 그림이다. 아래 두 그림은 원래 함수 f가 일대일대응이 아니었기 때문에 새로 만든 대응 관계는 함수가 아님을 확인할 수 있다.>

 그림의 위쪽은 일대일대응인 함수 f를 이용하여 역함수 g를 만든 그림입니다. f의 정의역은 g의 공역이 되고, f의 공역은 g의 정의역이 되었음을 알 수 있습니다. f의 정의역의 모든 원소는 각각 g의 정의역의 모든 원소 하나씩에 대응되기 때문에 새로운 함수 g의 정의역인 set E의 모든 원소도 새로운 공역인 set D의 원소 하나하나에 대응되는 것을 확인할 수 있습니다.

 

 하지만 일대일대응이 아닌 함수는 어떨까요? 두번째 그림은 원래 함수f가 일대일대응은 아니지만 일대일 함수인 경우입니다. 이 경우 정의역과 공역을 서로 바꾸어 주었을 때, 새로운 정의역이 된 set E의 원소 f(a)에 대응하는 set D의 원소가 없는 것을 확인할 수 있습니다. 일대일함수는 공역의 모든 원소가 정의역의 원소와 대응되어야 하는 것은 아니기 때문에, 역함수를 만들려고 시도할 때 새로운 정의역의 일부 원소는 대응되는 공역의 원소가 없는 상황이 발생하는 것입니다. 이 경우 함수의 정의에 어긋나므로 함수가 아니게 됩니다.

 

 마지막 그림은 두 정의역의 원소에 하나의 공역의 원소가 대응되는 경우입니다. 이 경우 정의역과 공역을 서로 뒤바꾸어 새로운 함수를 만들려 시도할 경우 새로운 정의역의 원소 하나가 서로 다른 공역의 여러 원소에 대응되는 일이 발생합니다. 이 경우 정의역의 원소에는 하나의 공역의 원소만 대응된다는 함수의 정의에 어긋나므로 함수가 아니게 됩니다.

 

 따라서 오직 일대일대응만 역함수를 가질 수 있다는 것을 확인할 수 있습니다.

 

---

3. 전사함수, 단사함수, 전단사함수

 일대일함수, 일대일대응과 비슷한 용어들이 있습니다. 바로 전사함수, 단사함수, 전단사함수 입니다. 그럼 이 용어들은 무엇을 가리키는 말인지 알아보겠습니다.

 

단사함수(injective function): 일대일함수

전사함수(surjective function):공역과 치역이 같은 함수

전단사함수(bijective function):일대일대응

 

그러니까, 단사함수=일대일함수, 전단사함수=일대일대응 이라는 뜻입니다. 전사함수는 위에서 설명되지 않은 개념입니다. 아래 그림을 보겠습니다.

<전사함수이지만 전단사함수(일대일대응)는 아닌 그림>

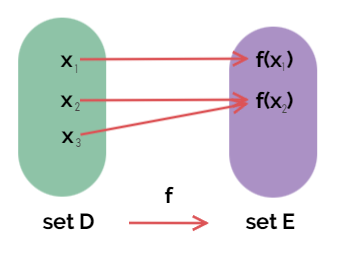
공역과 치역이 {f(x1), f(x2)}로 같기 때문에 이 함수는 전사함수입니다. 위 그림의 경우 전사함수이지만, 전단사함수=일대일대응 은 아닌 그림입니다. 공역과 치역이 같긴 하나, 일대일대응의 조건 (f(x1)=f(x2)이면 x1=x2) 를 만족하지 못하고 있기 때문입니다. x1과 x2 모두 f(x2)로 같은 함숫값을 가지나, 같은 정의역의 원소가 아니기 때문입니다. 

 

---

4.항등함수(identity function)와 상수함수(constant function)

 

 항등함수는 각 정의역의 원소에 자기 스스로가 대응되는 함수입니다. 정의를 살펴보겠습니다.

 

항등함수의 정의

함수 f:X->Y에서 정의역 X의 각 원소 x에 그 자신 x가 대응할 때, 즉 f(x)=x인 함수 f를 X에서의 항등함수라 한다.

 

<y=x 그래프>

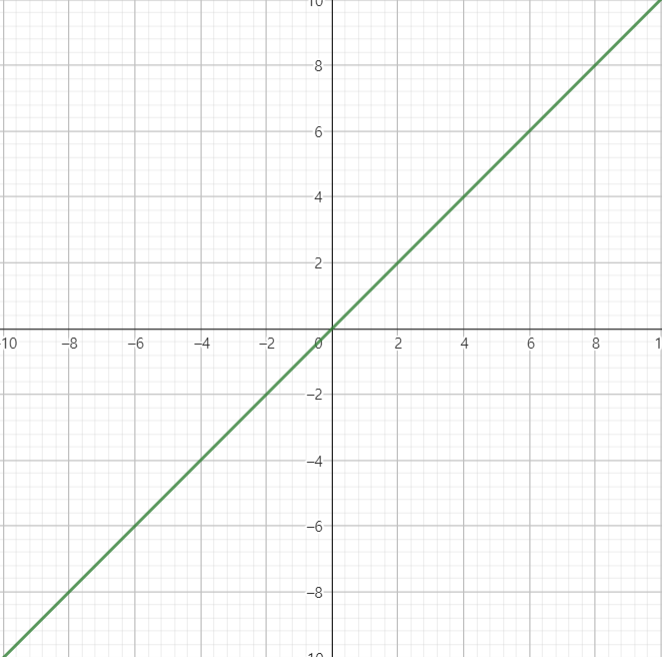
 항등함수는 단 한개 뿐입니다. 다른 항등함수가 존재할 수는 없습니다.

 

 

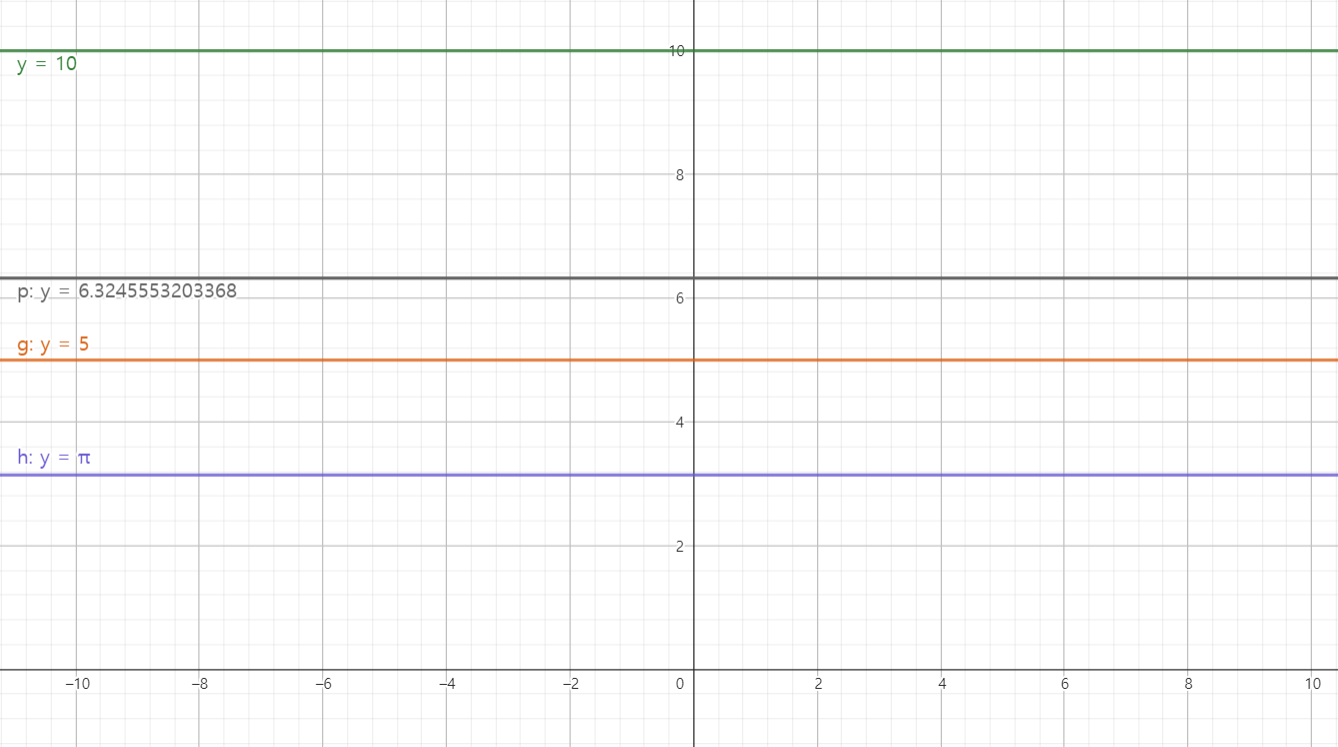
다음은 상수함수입니다. 상수함수는 말 그대로 정의역의 모든 원소가 공역의 한 원소에 대응되는 것입니다.

 

상수함수의 정의

함수 f:X->Y 에서 정의역 X의 모든 원소에 공역 Y의 단 하나의 원소 c만 대응할 때, 즉 f(x)=c 일 때 (c는 상수)  이 함수 f를 상수함수라 한다.

 

상수함수는 수평선과 같은 그래프를 갖게 됩니다.

 

<여러가지 상수함수의 그래프>

 

 

---

3. 함수의 개수 (일대일함수, 일대일대응의 개수)

 

함수 f: D->E 에서 집합 D의 원소가 m개, 집합 Y의 원소가 n개일 때, 함수의 개수는 아래와 같습니다.

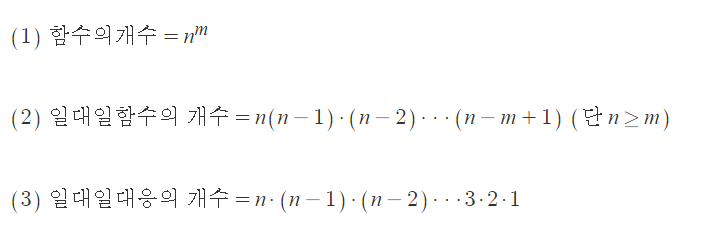
함수의 개수가 위와 같은 식으로 표현되는 이유에 대해 알아보겠습니다.

 

(1) 먼저 일반적인 함수의 개수입니다. 총 m개의 정의역의 원소를 ㅜ개의 공역의 원소 중 하나에 대응시키는 경우라고 생각하면 되겠습니다. 확률과 통계를 공부하셨다면 바로 알아차리셨을 텐데요, 네 맞습니다. 바로 중복순열을 적용시키는 경우입니다. 각각의 정의역의 원소마다 총 n개의 선택지가 있으니, n을 m번 곱해준 것이 바로 함수의 개수 , 즉 중복순열을 적용한

이 되는 것입니다. 

 

 

(2) 일대일함수의 경우는 조금 더 복잡합니다. 그러나 이렇게 생각하면 간단한데요. 맨 처음 정의역의 원소를 공역에 대응시킬 때는 총 n개의 선택지가 있지만, 한번 대응시킬때마다 선택지가 하나씩 줄어드는 것입니다. 네 맞습니다. 바로 순열인데요, 따라서 점점 선택지가 줄어들다가 마지막엔 공역의 원소 n개 중 이미 선택한m-1개의 원소를 제외한 선택지 중에서 하나를 고르는 경우가 되므로 위와 같은 식이 됩니다. 간단하게는 nPm,

 

 

(3) 일대일 대응도 일대일함수와 비슷하지만, n=m으로 정의역과 공역(치역)의 원소가 같다는 것이 다릅니다. 따라서 이같은 경우는 단순하게 n!=m! 개의 함수가 존재할 수 있게 되는 것이죠.

 

 

이상으로 이번 글에서는 여러가지 함수의 종류에 대해 알아보았습니다. 다음은 함수의 극한에 대한 글을 써보려 하니 많은 관심 부탁드립니다.